【人気ダウンロード!】 y=ax二乗 171575-Y=ax二乗 身の回り
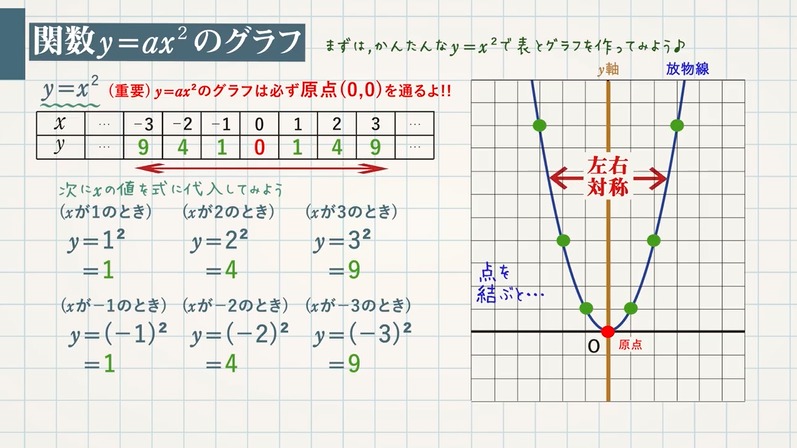
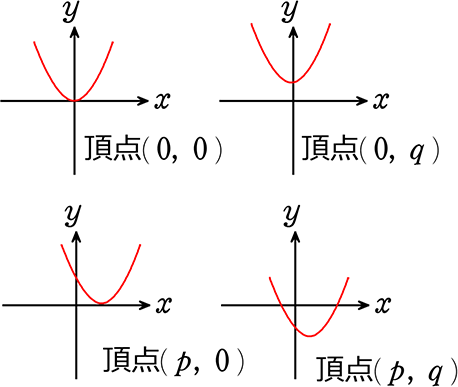
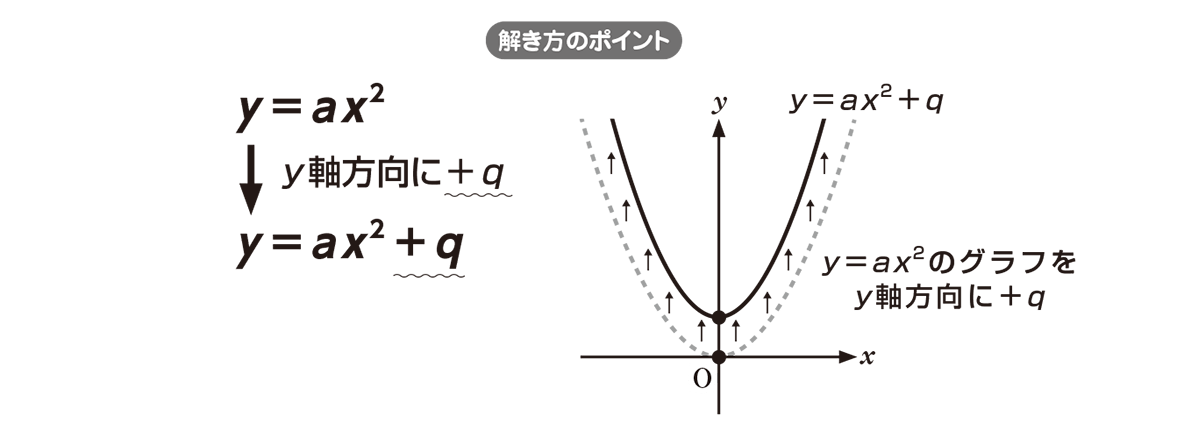
二次関数 y = a x 2 b x c のグラフをかくためには、まず頂点を求める必要がありました。 つまり、 y = a ( x − p) 2 q の形に式変形をする必要がある、ということです。 このよ
Y=ax二乗 身の回り-最小二乗法(直線)の簡単な説明 最小二乗法とは, データの組 (x_i,y_i) (xi,yi) が複数与えられたときに, x x と y y の関係を表す もっともらしい関数 y=f (x) y = f (x) を求める方法です。 この記事 最小二乗法y=axbのa,b導出方法についてメモする 回帰分析で用いる、最小二乗法の原理をメモする。 どのようにして添え字の量(回帰係数)が導出されるかを記載。 x を食べる量
Y=ax二乗 身の回りのギャラリー
各画像をクリックすると、ダウンロードまたは拡大表示できます
 |  | |
 |  |  |
 |  |  |
 |  | |
「Y=ax二乗 身の回り」の画像ギャラリー、詳細は各画像をクリックしてください。
 | ||
 | 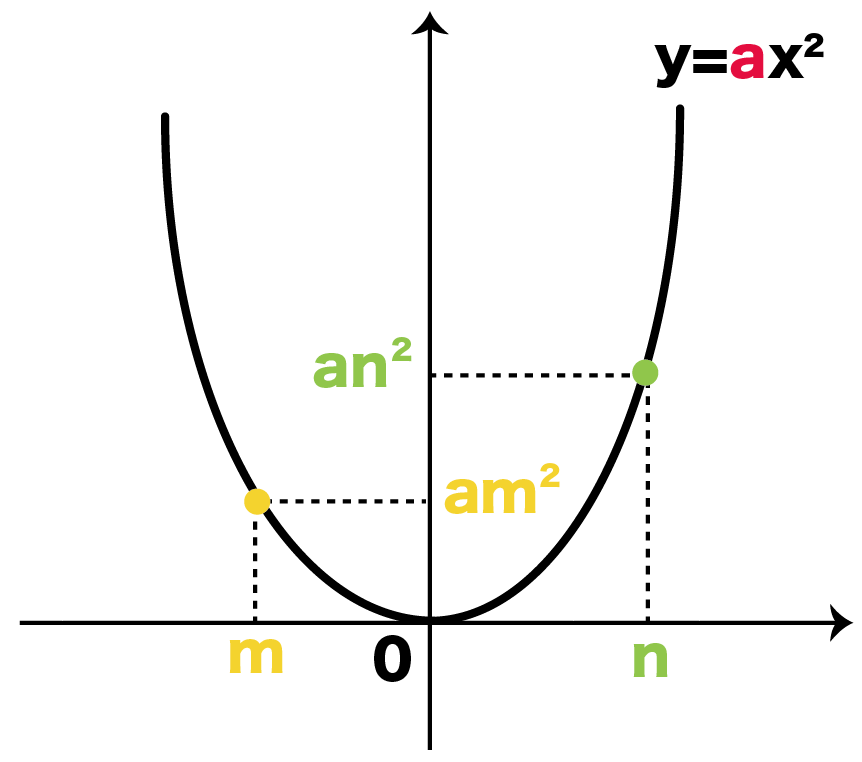 |  |
 |  | |
 |  |  |
「Y=ax二乗 身の回り」の画像ギャラリー、詳細は各画像をクリックしてください。
 | ||
 |  | |
 |  | |
 |  | |
「Y=ax二乗 身の回り」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  | |
 | ||
「Y=ax二乗 身の回り」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  |  |
 |  | |
 |  | |
「Y=ax二乗 身の回り」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  |  |
 |  |  |
 |  |  |
「Y=ax二乗 身の回り」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 |  |  |
 |  | |
「Y=ax二乗 身の回り」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  | |
 |  | |
 |  |  |
「Y=ax二乗 身の回り」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 | ||
 |  |
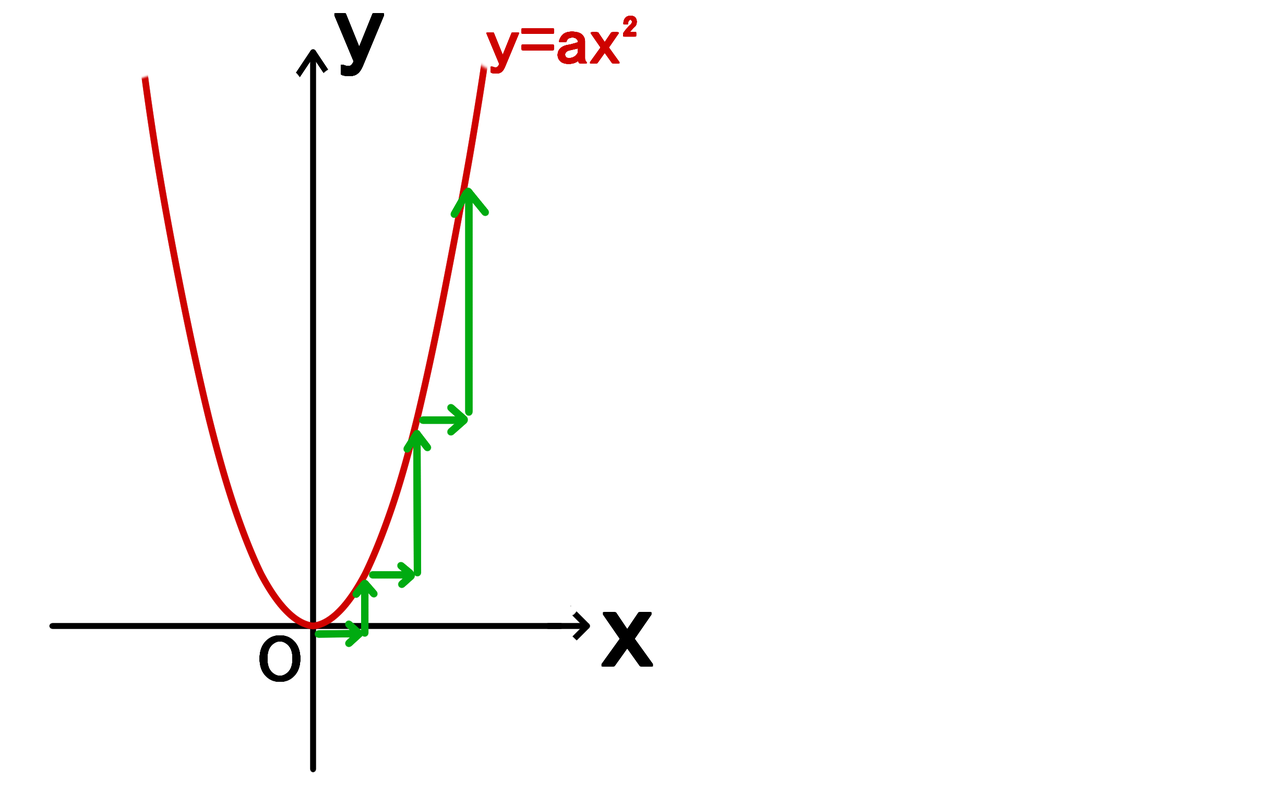
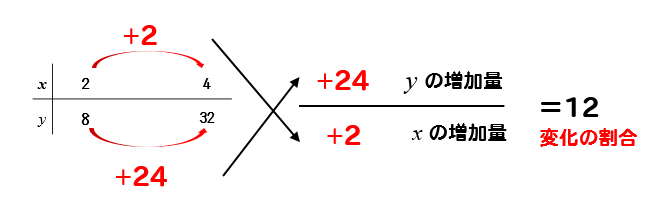
(yの増加量)÷(xの増加量) という割り算で求められます。 ( "割り" あいなので、 割り算 ですね!) y=ax² は曲線ですが、 上記の式は曲線にも使えるので、 気にする必要はありません。 簡単に 最小二乗法とは、誤差を伴う測定値の処理において、その誤差(残差)の二乗の和を最小にすることで最も確からしい関係式を求めることである。 プロットされた各点(x i, y i)における回
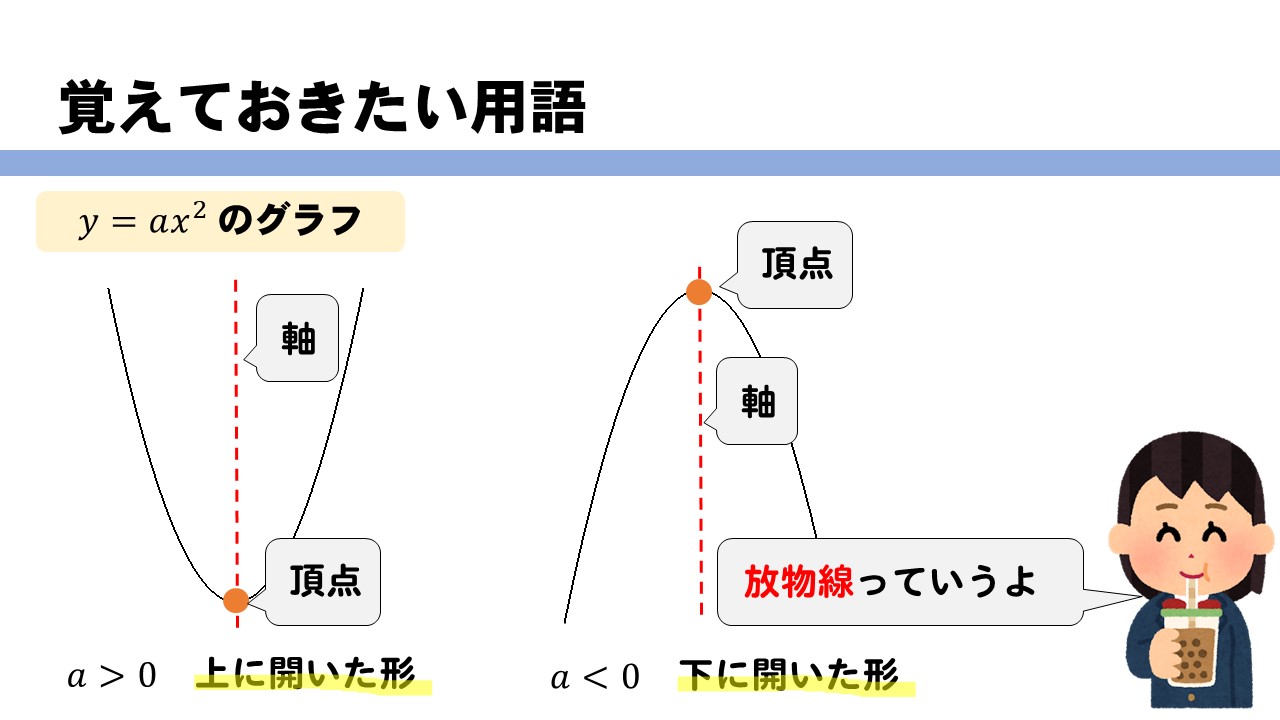
Incoming Term: y=ax二乗, y=ax二乗のグラフ, y=ax二乗 変化の割合, y=ax二乗+bx+c, y=ax二乗 特徴, y=ax二乗 身の回り, y=ax二乗 変域, y=ax二乗 aの求め方, y=ax二乗+b, y=ax二乗+bx+c 平方完成,
コメント
コメントを投稿